How to Read Multiple Regression Output Spss
This folio shows an example regression analysis with footnotes explaining the output. These information (hsb2) were collected on 200 loftier schools students and are scores on various tests, including science, math, reading and social studies (socst). The variable female is a dichotomous variable coded one if the student was female person and 0 if male.
In the syntax below, the get file control is used to load the information into SPSS. In quotes, you need to specify where the data file is located on your computer. Retrieve that you need to employ the .sav extension and that you demand to finish the control with a menstruation. In the regression control, the statistics subcommand must come up before the dependent subcommand. You can shorten dependent to dep. Yous list the independent variables later the equals sign on the method subcommand. The statistics subcommand is non needed to run the regression, only on it we can specify options that we would like to have included in the output. Here, we take specified ci, which is short for confidence intervals. These are very useful for interpreting the output, every bit we will run across. There are four tables given in the output. SPSS has provided some superscripts (a, b, etc.) to aid you in agreement the output.
Please note that SPSS sometimes includes footnotes as role of the output. We have left those intact and have started ours with the adjacent alphabetic character of the alphabet.
get file "c:\data\hsb2.sav". regression /statistics coeff outs r anova ci /dependent scientific discipline /method = enter math female socst read.
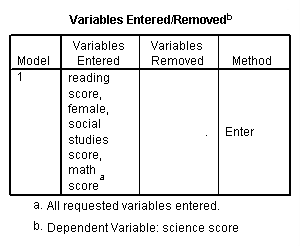


Variables in the model

c. Model – SPSS allows you to specify multiple models in a single regression command. This tells you the number of the model being reported.
d. Variables Entered – SPSS allows you to enter variables into a regression in blocks, and it allows stepwise regression. Hence, you demand to know which variables were entered into the electric current regression. If you did not block your contained variables or utilise stepwise regression, this column should listing all of the independent variables that y'all specified.
east. Variables Removed – This column listed the variables that were removed from the current regression. Commonly, this column will be empty unless you lot did a stepwise regression.
f. Method – This column tells yous the method that SPSS used to run the regression. "Enter" means that each independent variable was entered in usual fashion. If y'all did a stepwise regression, the entry in this cavalcade would tell y'all that.
Overall Model Fit
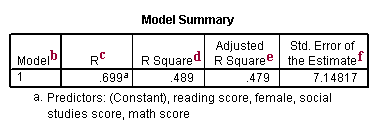
b. Model – SPSS allows you to specify multiple models in a single regression command. This tells you lot the number of the model beingness reported.
c. R – R is the square root of R-Squared and is the correlation between the observed and predicted values of dependent variable.
d. R-Square – R-Square is the proportion of variance in the dependent variable (science) which can be predicted from the contained variables (math, female person, socst and read). This value indicates that 48.ix% of the variance in science scores can be predicted from the variables math, female, socst and read. Note that this is an overall mensurate of the strength of clan, and does not reflect the extent to which whatsoever particular independent variable is associated with the dependent variable. R-Square is also called the coefficient of determination.
eastward. Adjusted R-square – As predictors are added to the model, each predictor volition explicate some of the variance in the dependent variable simply due to chance. Ane could proceed to add predictors to the model which would go on to better the power of the predictors to explain the dependent variable, although some of this increase in R-foursquare would be merely due to chance variation in that particular sample. The adjusted R-foursquare attempts to yield a more honest value to estimate the R-squared for the population. The value of R-square was .489, while the value of Adjusted R-square was .479 Adjusted R-squared is computed using the formula 1 – ((ane – Rsq)(N – 1 )/ (Northward – k – ane)). From this formula, you lot can run across that when the number of observations is small and the number of predictors is large, at that place will be a much greater difference betwixt R-square and adjusted R-square (because the ratio of (North – 1) / (Northward – 1000 – one) volition be much greater than 1). Past dissimilarity, when the number of observations is very large compared to the number of predictors, the value of R-square and adjusted R-square will be much closer because the ratio of (N – 1)/(North – grand – 1) will approach 1.
f. Std. Error of the Estimate – The standard error of the estimate, also called the root hateful square fault, is the standard deviation of the error term, and is the square root of the Hateful Square Residual (or Error).
Anova Table
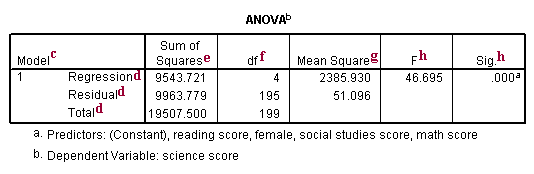
c. Model – SPSS allows y'all to specify multiple models in a single regression control. This tells yous the number of the model being reported.
d. This is the source of variance, Regression, Residual and Total. The Total variance is partitioned into the variance which tin can exist explained by the independent variables (Regression) and the variance which is non explained past the independent variables (Balance, sometimes called Error). Annotation that the Sums of Squares for the Regression and Residue add upwards to the Total, reflecting the fact that the Full is partitioned into Regression and Residual variance.
e. Sum of Squares – These are the Sum of Squares associated with the iii sources of variance, Total, Model and Residual. These tin can be computed in many ways. Conceptually, these formulas tin be expressed as: SSTotal The total variability around the mean. S(Y – Ybar)2. SSResidual The sum of squared errors in prediction. S(Y – Ypredicted)2. SSRegression The improvement in prediction by using the predicted value of Y over just using the mean of Y. Hence, this would be the squared differences between the predicted value of Y and the mean of Y, S(Ypredicted – Ybar)two. Another way to recall of this is the SSRegression is SSTotal – SSResidual. Note that the SSTotal = SSRegression + SSResidual. Note that SSRegression / SSTotal is equal to .489, the value of R-Square. This is because R-Square is the proportion of the variance explained by the independent variables, hence can be computed by SSRegression / SSTotal.
f. df – These are the degrees of freedom associated with the sources of variance. The total variance has N-1 degrees of freedom. In this case, there were North=200 students, then the DF for total is 199. The model degrees of freedom corresponds to the number of predictors minus 1 (K-1). Yous may think this would be 4-one (since there were 4 independent variables in the model, math, female, socst and read). But, the intercept is automatically included in the model (unless you explicitly omit the intercept). Including the intercept, there are 5 predictors, so the model has 5-1=four degrees of liberty. The Residual degrees of freedom is the DF total minus the DF model, 199 – four is 195.
g. Mean Foursquare – These are the Mean Squares, the Sum of Squares divided by their respective DF. For the Regression,
9543.72074 / 4 = 2385.93019. For the Residue, 9963.77926 / 195 =
51.0963039. These are computed and so you tin compute the F ratio, dividing the Mean Square Regression past the Mean Foursquare Residuum to examination the significance of the predictors in the model.
h. F and Sig. – The F-value is the Mean Square Regression (2385.93019) divided by the Mean Square Residue (51.0963039), yielding F=46.69. The p-value associated with this F value is very pocket-size (0.0000). These values are used to respond the question "Do the contained variables reliably predict the dependent variable?". The p-value is compared to your blastoff level (typically 0.05) and, if smaller, yous can conclude "Yes, the independent variables reliably predict the dependent variable". You could say that the group of variables math, and female, socst and read can exist used to reliably predict science (the dependent variable). If the p-value were greater than 0.05, y'all would say that the group of contained variables does non testify a statistically significant human relationship with the dependent variable, or that the group of contained variables does non reliably predict the dependent variable. Note that this is an overall significance test assessing whether the grouping of contained variables when used together reliably predict the dependent variable, and does non address the power of any of the item independent variables to predict the dependent variable. The power of each individual independent variable to predict the dependent variable is addressed in the table below where each of the individual variables are listed.
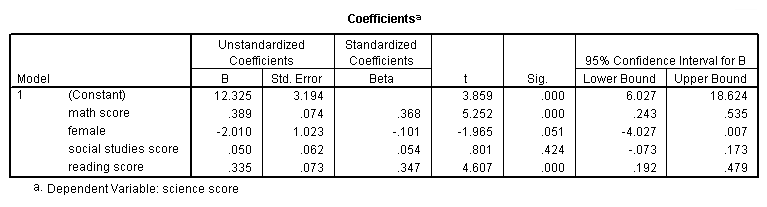
Parameter Estimates
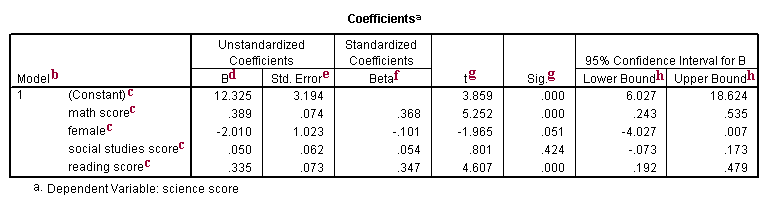
b. Model – SPSS allows y'all to specify multiple models in a single regression control. This tells you the number of the model being reported.
c. This cavalcade shows the predictor variables (constant, math, female, socst, read). The first variable (constant) represents the abiding, also referred to in textbooks as the Y intercept, the meridian of the regression line when it crosses the Y centrality. In other words, this is the predicted value of science when all other variables are 0.
d. B – These are the values for the regression equation for predicting the dependent variable from the independent variable. These are called unstandardized coefficients because they are measured in their natural units. As such, the coefficients cannot be compared with one some other to make up one's mind which one is more influential in the model, because they tin be measured on unlike scales. For example, how can you compare the values for gender with the values for reading scores? The regression equation tin can be presented in many different ways, for example:
Ypredicted = b0 + b1*x1 + b2*x2 + b3*x3 + b3*x3 + b4*x4
The cavalcade of estimates (coefficients or parameter estimates, from here on labeled coefficients) provides the values for b0, b1, b2, b3 and b4 for this equation. Expressed in terms of the variables used in this example, the regression equation is
sciencePredicted = 12.325 +
.389*math + -two.010*female person+.050*socst+.335*read
These estimates tell yous about the relationship between the independent variables and the dependent variable. These estimates tell the amount of increment in science scores that would exist predicted by a 1 unit increase in the predictor. Notation: For the independent variables which are not pregnant, the coefficients are not significantly different from 0, which should be taken into business relationship when interpreting the coefficients. (Meet the columns with the t-value and p-value almost testing whether the coefficients are pregnant). math – The coefficient (parameter approximate) is
.389. And so, for every unit (i.e., betoken, since this is the metric in which the tests are measured) increase in math, a .389 unit increase in scientific discipline is predicted, holding all other variables constant. (It does not matter at what value y'all concur the other variables constant, because information technology is a linear model.) Or, for every increase of 1 point on the math test, your science score is predicted to be higher by .389 points. This is significantly different from 0. female – For every unit increase in female person, there is a
-2.010 unit decrease in the predicted science score, holding all other variables constant. Since female person is coded 0/1 (0=male person, ane=female) the interpretation can exist put more than only. For females the predicted science score would exist 2 points lower than for males. The variable female is technically not statistically significantly different from 0, because the p-value is greater than .05. All the same, .051 is so close to .05 that some researchers would still consider it to exist statistically pregnant. socst – The coefficient for socst is .050. This means that for a 1-unit increase in the social studies score, we expect an approximately .05 bespeak increase in the scientific discipline score. This is not statistically meaning; in other words, .050 is not dissimilar from 0. read – The coefficient for read is .335. Hence, for every unit increase in reading score nosotros expect a .335 signal increment in the scientific discipline score. This is statistically significant.
e. Std. Mistake – These are the standard errors associated with the coefficients. The standard mistake is used for testing whether the parameter is significantly dissimilar from 0 by dividing the parameter estimate past the standard error to obtain a t-value (see the column with t-values and p-values). The standard errors can also be used to grade a confidence interval for the parameter, every bit shown in the last two columns of this table.
f. Beta – These are the standardized coefficients. These are the coefficients that you would obtain if you standardized all of the variables in the regression, including the dependent and all of the independent variables, and ran the regression. By standardizing the variables before running the regression, you have put all of the variables on the same scale, and you can compare the magnitude of the coefficients to see which one has more than of an result. Y'all will also notice that the larger betas are associated with the larger t-values.
1000. t and Sig. – These columns provide the t-value and ii tailed p-value used in testing the null hypothesis that the coefficient/parameter is 0. If yous use a 2 tailed test, then y'all would compare each p-value to your preselected value of blastoff. Coefficients having p-values less than alpha are statistically pregnant. For example, if you lot chose alpha to be 0.05, coefficients having a p-value of 0.05 or less would be statistically significant (i.e., yous can reject the null hypothesis and say that the coefficient is significantly different from 0). If you utilize a i tailed examination (i.e., y'all predict that the parameter volition get in a particular direction), then y'all can divide the p-value by 2 before comparing it to your preselected blastoff level. With a 2-tailed test and alpha of 0.05, y'all should not reject the naught hypothesis that the coefficient for female person is equal to 0, because p-value = 0.051 > 0.05. The coefficient of -two.009765 is not significantly different from 0. However, if yous hypothesized specifically that males had higher scores than females (a 1-tailed test) and used an alpha of 0.05, the p-value of .0255 is less than 0.05 and the coefficient for female would exist significant at the 0.05 level. In this example, we could say that the female coefficient is significantly greater than 0. Neither a ane-tailed nor 2-tailed test would exist meaning at alpha of 0.01.
The constant is significantly unlike from 0 at the 0.05 alpha level. Yet, having a significant intercept is seldom interesting.
The coefficient for math (.389) is statistically significantly dissimilar from 0 using alpha of 0.05 because its p-value is 0.000, which is smaller than 0.05.
The coefficient for female (-two.01) is not statistically significant at the 0.05 level since the p-value is greater than .05.
The coefficient for socst (.05) is not statistically significantly different from 0 considering its p-value is definitely larger than 0.05.
The coefficient for read (.335) is statistically significant because its p-value of 0.000 is less than .05.
h. [95% Conf. Interval] – These are the 95% confidence intervals for the coefficients. The confidence intervals are related to the p-values such that the coefficient will not be statistically significant at alpha = .05 if the 95% confidence interval includes zero. These confidence intervals can aid you to put the estimate from the coefficient into perspective by seeing how much the value could vary.
grossmanhaideatel.blogspot.com
Source: https://stats.oarc.ucla.edu/spss/output/regression-analysis/
0 Response to "How to Read Multiple Regression Output Spss"
Post a Comment